L'avancement de l'intelligence artificielle dépasse à nouveau les limites de l'imagination. Cette fois, le protagoniste est la démonstration mathématique. Récemment, des chercheurs d'OpenAI ont révélé une découverte qui a secoué toute la communauté académique : GPT-5Pro, après avoir lu un article de mathématiques, a réussi à dériver des conclusions mathématiques plus précises que celles du texte original et à fournir un processus complet de preuve. Cette nouvelle s'est propagée comme un feu de forêt, et les publications sur les réseaux sociaux ont atteint plus de 2,3 millions de lectures en moins d'une demi-journée, déclenchant un débat passionné sur Internet.
Une percée historique dans la démonstration mathématique
La cause de l'événement semblait banale. Un chercheur d'OpenAI a entré un article académique sur un problème d'optimisation convexe dans GPT-5Pro, tout simplement pour tester la compréhension du modèle. Cependant, personne ne s'attendait à ce que GPT-5Pro, après avoir lu attentivement le contenu de l'article, fournisse un seuil plus précis qu'original concernant un problème de borne, accompagné d'un processus de preuve mathématique rigoureux.
Cette découverte va bien au-delà de ce qui semble être apparent. Elle signifie que l'IA n'est plus seulement un répétiteur ou un organisateur des connaissances humaines, mais qu'elle possède véritablement la capacité de penser indépendamment et de raisonner de manière innovante. GPT-5Pro ne recherchait pas simplement des réponses dans une base de connaissances existante, mais utilisait la logique mathématique pour effectuer des raisonnements originaux. L'apparition de cette capacité marque un point de bascule important dans le développement de l'intelligence artificielle.
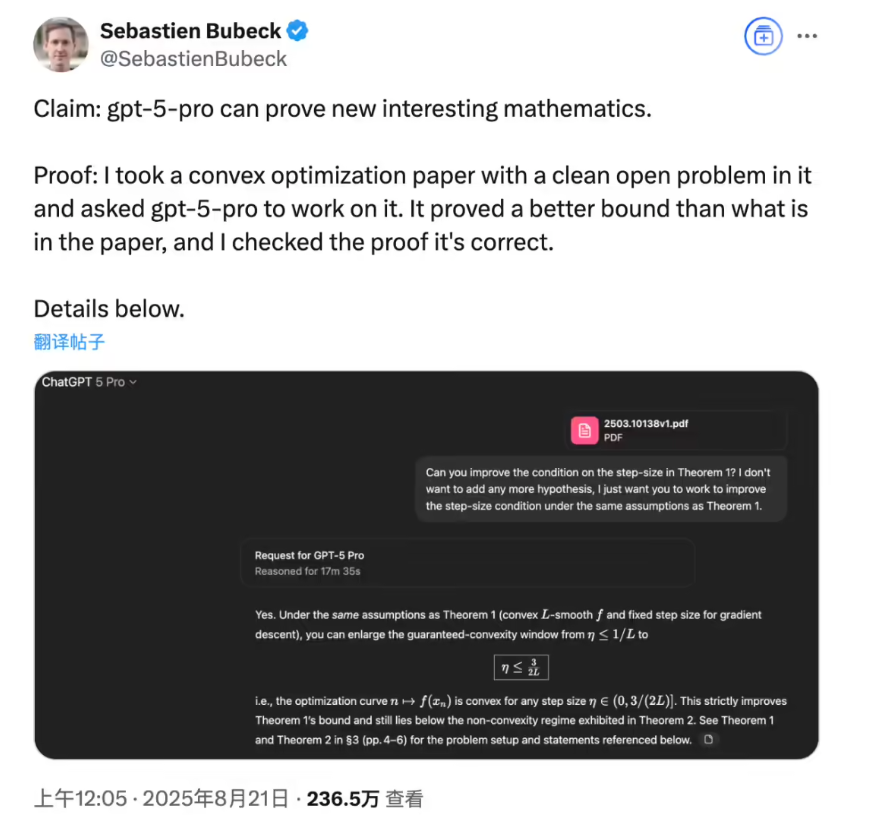
Même si le chercheur n'a finalement pas publié les résultats de GPT-5Pro sous forme d'article officiel, la raison était assez dramatique. Juste avant la publication, l'auteur original a publié une version mise à jour, donnant un nouveau résultat de borne, qui surpassait même la découverte de GPT-5Pro. La riposte rapide des chercheurs humains a montré le niveau élevé de compétitivité dans le domaine académique.
Cependant, la découverte la plus importante réside dans la méthode de preuve de GPT-5Pro, qui diffère entièrement de celle des chercheurs humains. Cette différence prouve que l'IA n'est pas simplement une imitation ou une copie, mais qu'elle possède réellement la capacité d'explorer indépendamment et d'innover. Comme l'a déclaré Brockman, président d'OpenAI, ce comportement est considéré comme un « signe de vie », suggérant que l'IA pourrait développer des caractéristiques d'intelligence similaires à celles des humains.
Les mystères mathématiques du problème d'optimisation convexe
L'article que GPT-5Pro a remis en question portait sur une question importante dans le domaine de l'optimisation convexe. L'optimisation convexe est une branche importante des mathématiques de l'optimisation, qui traite spécifiquement de la minimisation des fonctions convexes définies sur des ensembles convexes. Elle est largement utilisée dans des domaines tels que l'apprentissage automatique, l'économie et l'ingénierie.

L'article intitulé « Les courbes d'optimisation convexe sont-elles convexes ? » explore une question apparemment simple mais extrêmement importante : lorsque l'algorithme de descente de gradient est utilisé pour optimiser une fonction convexe lisse, la courbe d'optimisation est-elle convexe ? La courbe d'optimisation désigne la courbe représentant les valeurs de la fonction en fonction du nombre d'itérations. Si cette courbe est convexe, cela signifie que le taux d'optimisation diminue de manière monotone.
La découverte centrale de l'article porte sur l'effet de la sélection du pas. Les études montrent que la convexité de la courbe d'optimisation dépend entièrement du choix du pas. Lorsque le pas se situe dans une plage spécifique, la courbe d'optimisation garantit sa convexité ; cependant, lorsqu'il dépasse un certain seuil, même si l'algorithme de descente de gradient converge encore, la courbe d'optimisation peut perdre sa propriété de convexité.

Les performances remarquables de GPT-5Pro
Dans la première version de l'article, les auteurs ont réussi à prouver les cas où le pas est inférieur ou égal à 1/L et supérieur à 1,75/L, mais ont laissé un vide théorique dans la plage intermédiaire. C'est précisément dans ce domaine non exploré que GPT-5Pro a montré son incroyable sens mathématique.
GPT-5Pro a utilisé une technique d'inégalité plus fine pendant 17 minutes et 30 secondes, permettant de déplacer avec précision le seuil de 1/L à 1,5/L. En comparaison, les experts humains ont mis 25 minutes pour vérifier cette démonstration, prouvant ainsi que l'IA dépasse déjà les humains dans certains tâches de raisonnement mathématique.
Ce qui est encore plus impressionnant, c'est la stratégie de preuve adoptée par GPT-5Pro. Il a habilement utilisé deux inégalités fondamentales des fonctions convexes L-lisses : l'inégalité de divergence de Bregman et l'inégalité classique de coercivité. Grâce à des opérations algébriques subtiles, GPT-5Pro a réussi à affiner davantage les conditions de convexité, démontrant ainsi un solide savoir-faire mathématique et une pensée innovante.
La riposte humaine et l'originalité de l'IA
Un développement dramatique a suivi. Alors que les découvertes de GPT-5Pro attiraient l'attention, l'auteur original a rapidement mis à jour l'article, ajoutant un co-auteur et réussissant à prouver que 1,75/L est la valeur exacte du seuil, comblant complètement le vide théorique précédemment non exploré.
La méthode de preuve des chercheurs humains est également ingénieuse. Ils ont utilisé l'inégalité de divergence de Bregman des fonctions convexes L-lisses pour établir des inégalités pour trois paires de points différentes, puis ont combiné ces inégalités avec différents poids, simplifiant habilement les termes de gradient complexes grâce à une identité, pour obtenir finalement une limite mathématique précise.
Même si les chercheurs humains ont finalement gagné sur le plan mathématique, la méthode de preuve de GPT-5Pro diffère radicalement de celle de la nouvelle version de l'article, une différence qui a une importance significative. Cela montre que l'IA n'a pas prédit la direction des recherches humaines, mais qu'elle possède véritablement la capacité de raisonner mathématiquement de manière indépendante et innovante.
Le sens historique de la capacité mathématique de l'IA
La percée de GPT-5Pro dans la démonstration mathématique a un profond impact historique. C'est la première fois qu'un système d'IA démontre une capacité supérieure aux calculs simples et à la recherche de connaissances dans le domaine de la logique mathématique pure, pénétrant véritablement dans le domaine du raisonnement mathématique original.
Cette capacité aura un impact majeur sur plusieurs domaines. Dans le domaine de la recherche mathématique, l'IA pourra devenir un puissant assistant pour les mathématiciens, les aidant à explorer de nouveaux théorèmes et méthodes de preuve. Dans les domaines de l'ingénierie et des calculs scientifiques, la capacité de raisonnement mathématique de l'IA offrira de nouvelles idées pour résoudre des problèmes complexes. Dans le domaine de l'éducation, l'IA pourrait même révolutionner la façon dont les mathématiques sont enseignées et apprises.
Plus important encore, cette percée démontre le potentiel de l'IA en matière de pensée abstraite et de raisonnement logique. Une démonstration mathématique nécessite une chaîne logique rigoureuse, un angle de pensée innovant et une profonde compréhension. Les performances de GPT-5Pro dans ces aspects prouvent que l'IA se rapproche progressivement d'un niveau plus élevé d'intelligence.
Les possibilités infinies du futur
La capacité de GPT-5Pro à démontrer des mathématiques est un point important dans le parcours de développement de l'IA. Avec l'amélioration continue des capacités des modèles et l'optimisation constante des méthodes d'entraînement, nous pouvons raisonnablement espérer que l'IA fera des progrès dans de nombreux domaines nécessitant une pensée créative.
De la preuve de théorèmes mathématiques à la formulation d'hypothèses scientifiques, en passant par la résolution de problèmes d'ingénierie et la conception artistique, la capacité d'innovation de l'IA s'étend rapidement. Ce mouvement de tendance ne changera pas seulement notre compréhension de l'essence de l'intelligence artificielle, mais redéfinira aussi le mode de collaboration entre les humains et l'IA.
