Artificial intelligence's development has once again broken the boundaries of imagination, with mathematics proofs now at the center. Recently, OpenAI researchers revealed a discovery that shocked the entire academic community: GPT-5Pro not only read a mathematical paper but also independently derived a more accurate mathematical conclusion than the original text and provided a complete proof process. This news spread like wildfire, with related tweets receiving over 2.3 million views within half a day, sparking widespread online discussions.
A Historic Breakthrough in Mathematical Proofs
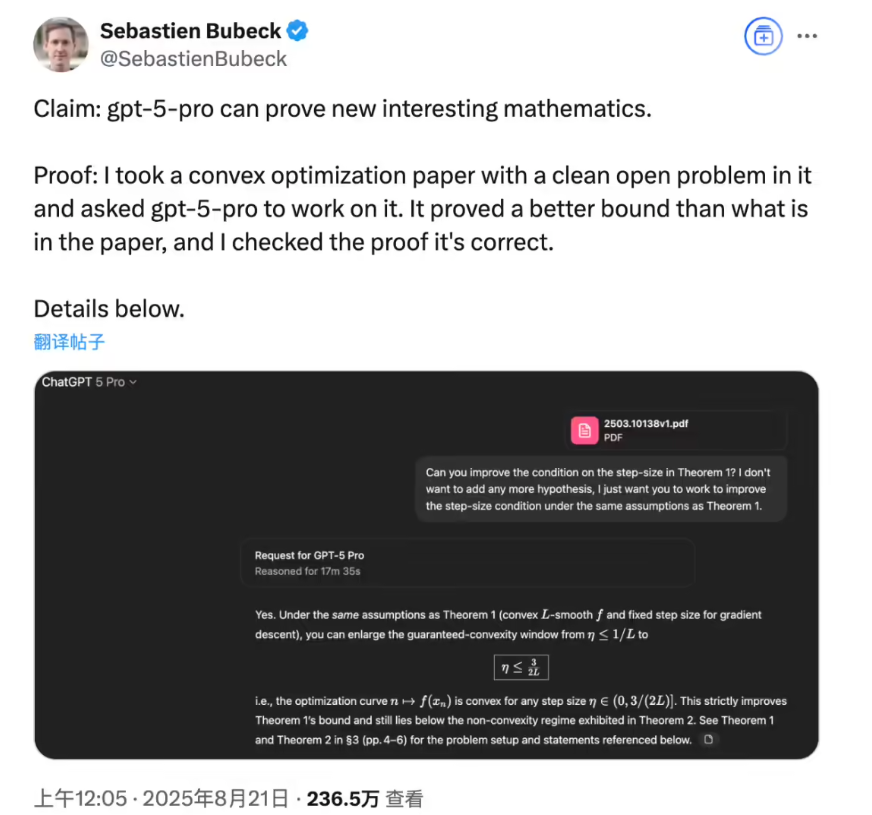
The incident started seemingly normally. An OpenAI researcher input a paper on convex optimization problems into GPT-5Pro, initially just to test the model's understanding ability. However, to everyone's surprise, after carefully reading the content of the paper, GPT-5Pro provided a more precise threshold for one of the boundary issues and gave a rigorous mathematical proof process.
This discovery goes far beyond its surface appearance. It means that AI is no longer merely a repeater or organizer of human knowledge, but truly possesses the ability to think independently and reason creatively. GPT-5Pro was not searching for answers in an existing knowledge base, but using mathematical logic to conduct original derivations. The emergence of this ability marks an important turning point in AI development.
Although the researcher ultimately did not publish the research results of GPT-5Pro as a formal paper, the reason was quite dramatic. Just as they were preparing to publish, the original paper's author released an updated version, providing new boundary results, which exceeded GPT-5Pro's findings. The rapid response from human scholars demonstrated the intensity of academic competition.
However, the most critical finding lies in the fact that GPT-5Pro's proof approach was completely different from that of human scholars. This difference proves that AI is not simply imitating or copying, but truly possesses the ability to explore and innovate independently. As OpenAI's president Brockman said, this performance is akin to a "sign of life," implying that AI may be developing characteristics similar to human intelligence.
The Mathematical Secrets of Convex Optimization Problems
GPT-5Pro challenged a paper that studied an important issue in the field of convex optimization. As an essential branch of mathematical optimization, convex optimization focuses on minimizing convex functions defined on convex sets, with wide applications in machine learning, economics, engineering, and other fields.

The paper, titled "Is the Convex Optimization Curve Convex?" explores a seemingly simple yet extremely important question: when using gradient descent algorithms to optimize smooth convex functions, does the resulting optimization curve have convexity? Here, the optimization curve refers to the curve of function values changing with the number of iterations. If this curve is convex, it means that the optimization rate shows a monotonically decreasing trend.
The core discovery of the paper revolves around the impact of step size selection. The study showed that the convexity of the optimization curve depends entirely on the setting of the step size. When the step size is within a specific range, the convexity of the optimization curve can be guaranteed; however, when the step size exceeds a certain threshold, even if the gradient descent algorithm still converges, the optimization curve may lose its convexity characteristics.

GPT-5Pro's Outstanding Performance
In the first version of the original paper, the authors successfully proved the cases where the step size was not greater than 1/L and greater than 1.75/L, but left a theoretical gap in the intermediate interval. It was in this unexplored area that GPT-5Pro demonstrated its extraordinary mathematical insight.
GPT-5Pro managed to move the boundary of 1/L to 1.5/L by employing more refined inequality techniques in just 17 and a half minutes. In contrast, human experts spent 25 minutes checking this proof, proving that AI has surpassed humans in processing speed for certain mathematical reasoning tasks.
More impressively, the proof strategy used by GPT-5Pro was remarkable. It skillfully applied two fundamental inequalities of convex L-smooth functions: Bregman divergence inequality and the standard monotonicity inequality. Through clever algebraic operations, GPT-5Pro successfully refined the convexity condition, showcasing profound mathematical expertise and innovative thinking.
The Human Counterattack and AI's Originality
Subsequently, a dramatic turn of events occurred. As the discovery of GPT-5Pro gained attention, the original paper's authors quickly updated the paper version, adding a co-author and successfully proving that 1.75/L is the exact boundary value, completely filling the previously unexplored theoretical gap.
The human scholars' proof approach was equally ingenious. They utilized the Bregman divergence inequality of convex L-smooth functions, establishing inequalities for three different pairs of points, then summing these inequalities with different weights, and through identities, they cleverly simplified complex gradient terms, ultimately obtaining the exact mathematical boundary.
Although the human scholars eventually regained ground in mathematical results, GPT-5Pro's proof approach was entirely different from the updated paper, a difference of great significance. It indicates that AI did not somehow know the direction of human research, but truly possesses independent mathematical reasoning and innovation capabilities.
The Milestone Significance of AI's Mathematical Ability
The breakthrough of GPT-5Pro in mathematical proofs carries profound historical significance. This is the first time an AI system has shown abilities that go beyond simple computation and knowledge retrieval in the field of pure mathematical reasoning, entering the realm of original mathematical thinking.
The emergence of this ability will have a significant impact on multiple fields. In the field of mathematical research, AI can become a powerful assistant for mathematicians, helping to explore new theorems and proof methods. In engineering and scientific computing, AI's mathematical reasoning ability will provide new ideas for solving complex problems. In education, AI may even revolutionize the way mathematics is taught and learned.
More importantly, this breakthrough demonstrates the potential of AI in abstract thinking and logical reasoning. Mathematical proofs require a strict logical chain, innovative thinking angles, and deep insights, and GPT-5Pro's performance in these aspects proves that AI is moving towards a higher level of intelligence.
The Infinite Possibilities of the Future
GPT-5Pro's ability to prove mathematics is just an important milestone in AI's development journey. With the continuous improvement of model capabilities and the ongoing optimization of training methods, we have every reason to expect AI to make breakthroughs in more fields that require innovative thinking.
From proving mathematical theorems to proposing scientific hypotheses, from solving engineering problems to brainstorming artistic creations, AI's innovative capabilities are rapidly expanding. This developmental trend not only changes our understanding of the essence of artificial intelligence but also redefines the way humans and AI collaborate.









