Les grands modèles linguistiques (LLM) ont réalisé des progrès notables dans les tâches complexes de raisonnement en combinant des prompts d'entrée et un apprentissage par renforcement à grande échelle (RL), comme le modèle Deepseek-R1-Zero, qui applique directement l'apprentissage par renforcement au modèle de base, démontrant ainsi une forte capacité de raisonnement. Cependant, ce succès est difficile à reproduire dans différentes séries de modèles de base, notamment dans la série Llama. Cela soulève une question centrale : quels sont les facteurs qui provoquent des performances incohérentes des différents modèles de base lors du processus d'apprentissage par renforcement ?
Limites de l'extension de l'apprentissage par renforcement sur les modèles Llama
Des modèles tels que o1, o3 d'OpenAI et R1 de DeepSeek ont obtenu des percées dans les problèmes mathématiques de compétition grâce à un apprentissage par renforcement à grande échelle, poussant ainsi l'exploration des capacités d'apprentissage par renforcement des modèles de petite taille en dessous de plusieurs milliards de paramètres. Cependant, ces progrès sont principalement limités aux séries de modèles Qwen, rendant difficile leur réplication sur des modèles comme Llama. Le manque de transparence dans le processus de pré-entraînement rend difficile la compréhension de l'impact du pré-entraînement sur l'expansion de l'apprentissage par renforcement. Certaines recherches non conventionnelles ont constaté que des prompts uniques peuvent améliorer la capacité de raisonnement de Qwen, mais avec peu d'effet sur Llama. Bien que des projets tels qu'OpenWebMath et MathPile visent à rassembler des corpus de pré-entraînement mathématique de haute qualité, leur taille reste limitée à moins de plusieurs milliards de tokens.
Exploration d'une stratégie de décroissance stable pendant l'entraînement
Les chercheurs de l'Université de Shanghai Jiao Tong ont étudié les effets des stratégies d'entraînement intermédiaire sur la dynamique de l'apprentissage par renforcement, en se concentrant sur Qwen et Llama, et ont tiré les conclusions suivantes :
En premier lieu, des bases de données mathématiques de haute qualité comme MegaMath-Web-Pro améliorent à la fois les modèles de base et l'apprentissage par renforcement. Ensuite, l'utilisation de données sous forme de questions-réponses, particulièrement celles comportant des raisonnements CoT (chaîne de pensée) longs, peut encore renforcer l'apprentissage par renforcement. Troisièmement, les CoT longs introduisent de la longueur et de l'instabilité dans l'entraînement par renforcement. Enfin, l'application d'une extension pendant l'entraînement intermédiaire améliore les performances de l'apprentissage par renforcement ultérieur.
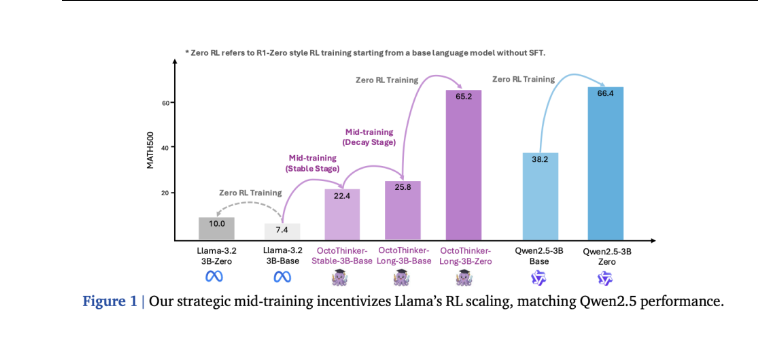
Les chercheurs ont proposé une stratégie d'entraînement intermédiaire à deux phases appelée "stabilité-décroissance" : tout d'abord, entraîner le modèle de base avec 200 milliards de tokens, puis utiliser 20 milliards de tokens pour l'entraînement sur trois branches centrées sur le CoT. Cette stratégie a finalement permis de générer le modèle OctoThinker, capable de s'adapter efficacement à l'apprentissage par renforcement.
Configuration RL et évaluation de benchmarks
Les chercheurs ont utilisé le jeu de données MATH8K pour l'entraînement par renforcement (RL), avec des configurations comprenant une taille globale de lot d'entraînement de 128, 16 réponses de rollout par requête et une taille minimale de lot PPO de 64. Les expériences ont été menées sur les modèles Llama-3.2-3B-Base et Qwen2.5-3B-Base. Lors de l'évaluation, les modèles de base ont utilisé des prompts à faible échantillon, tandis que les modèles optimisés par apprentissage par renforcement ont utilisé des prompts zéro échantillon sur des tâches d'évaluation telles que GSM8K, MATH500, OlympiadBench et AMC23.
Pendant l'entraînement par renforcement, la longueur des réponses de Qwen a constamment augmenté et resté dans une plage raisonnable, alors que le modèle Llama a montré un comportement anormal, avec une longueur moyenne de réponse qui a bondi à 4 096 tokens. Les résultats d'évaluation montrent également que le Qwen2.5-3B optimisé par apprentissage par renforcement a connu une amélioration sur tous les benchmarks, tandis que l'amélioration du Llama-3.2-3B a été minime.
OctoThinker dépasse Llama en termes de compatibilité RL
Dans 13 benchmarks mathématiques, chaque branche d'OctoThinker a amélioré le modèle de base Llama original de 10 à 20 %, et a obtenu des améliorations continues sur tous les modèles de phase stable de toutes les tailles. La série OctoThinker-Zero a montré des comportements de pensée variés pendant l'extension de l'apprentissage par renforcement, avec une performance particulièrement bonne pour la variante OctoThinker-Long. En comparant les trois modèles de base de 3B lors de l'entraînement par renforcement, OctoThinker-Long-3B a surpassé le modèle original Llama-3.2-3B, atteignant un niveau de performance similaire à celui du modèle Qwen2.5-3B, célèbre pour sa forte capacité de raisonnement et son pré-entraînement étendu. Les performances des branches mixtes et courtes étaient légèrement inférieures, surtout dans les benchmarks plus exigeants.
Résultats et travaux futurs : vers des modèles de base prêts pour RL
Cette étude a approfondi les raisons des différences de comportement des modèles de base tels que Llama et Qwen pendant le raisonnement par apprentissage par renforcement, et a souligné l'importance de l'entraînement intermédiaire pour l'expansibilité de l'apprentissage par renforcement. La stratégie d'entraînement intermédiaire à deux phases a réussi à transformer Llama en un modèle de base plus adapté à l'apprentissage par renforcement, aboutissant finalement au modèle OctoThinker.









